生成树
生成树是指在一个无向联通图上面保留 $V-1$ 条边,且保持联通。
因此图的生成树并不唯一。比如下图就是一个图的生成树
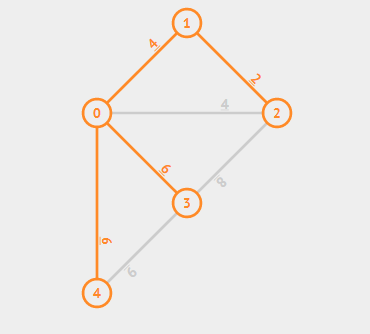
最小生成树
上文说过生成树不唯一,那么就一定会有生成树的大小。生成树上面的所有权值之和就是它的代价,代价最小的生成树则为最小生成树。最小生成树在实际生活中也有着很大的意义,比如“现在希望修建多条条公路联通几个城市,如何修路总里程最小呢?”
Prim
Prim 将生成树上的点集合 $V$ 分成两个部分:已经被联通的点和未被联通的点。该算法一直在重复在所有已经联通的点集合里面的点与在所有未被联通的点集合里面的点寻找最小的边 $u \rightarrow v$ 选定为是生成树的边。最后所有选中的边一定是 $V-1$ 个。
上面重复寻找的动作即为枚举。比如下面这个示例:
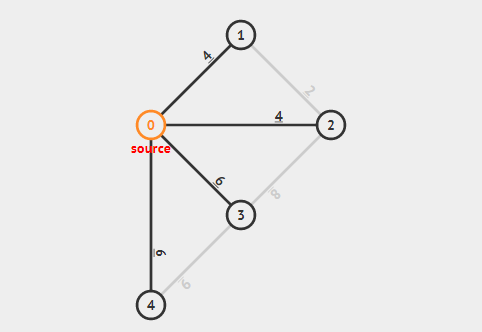
开始寻找所有能前往(就是还没被联通)的最小边。

找到当前最小的路径 $0 \rightarrow 1$ 为最小生成树的一个答案,继续寻找符合条件的最小边。
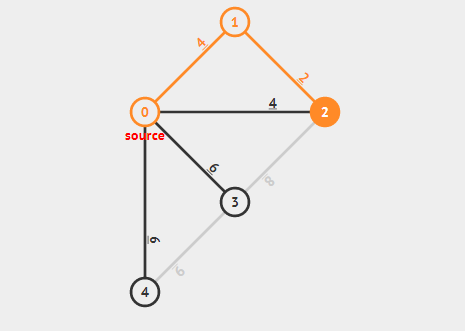
找到当前最小的路径 $1 \rightarrow 2$ 为最小生成树的一个答案,继续寻找符合条件的最小边。

找到当前最小的路径 $2 \rightarrow 0$ ,但 $0$ 已经是最小生成树的答案边所在点了,所以这个答案无效,继续寻找符合条件的最小边。
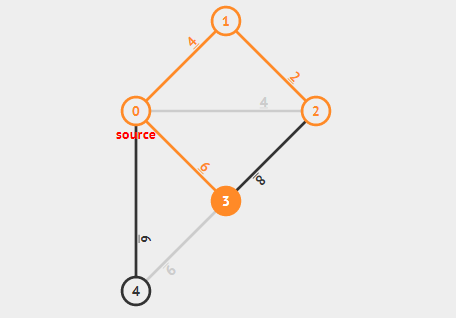
找到当前最小的路径 $0 \rightarrow 3$ 为最小生成树的一个答案,继续寻找符合条件的最小边。

找到当前最小的路径 $0 \rightarrow 4$ 为最小生成树的一个答案,现在已经联通了这个图,结束最小生成树寻找。
实现 Prim
根据上面的分析,我们就能写出代码了。
//初始化(adj数组是邻接矩阵表)
for (int i = 0; i <= n; i ++)
{
cost[i] = INT_MAX;
vis[i] = 0;
}
cost[1] = 0;
int res = 0;
//开始Prim
for (int i = 0; i < n; i ++)
{
//寻找可用的最下的边,并保存到index
int index = 0;
for (int j = 1; j <= n; j ++)
{
if (vis[j] == 0 && cost[j] < cost[index])
{
index = j;
}
}
vis[index] = 1; //将最小的点标记为访问过
res += cost[index]; //记录最小代价
for (int j = 1; j <= n; j ++)
{
if (vis[j] == 0 && cost[j] > adj[index][j])
{
cost[j] = adj[index][j];
}
}
}Kruskal
Kruskal的核心思想是通过贪心的方法来选择边。它的想法就是在所有边中一直寻找最小的边,但不能形成环状的就行,一旦最小生成树的边成为环状结构之后,它将不可能再联通了,证明很简单不再细说了。它的这种思想我们可以用并查集实现。
实现方法:
- 所有的边按照从小到大进行排列
- 如果边链接的两个点都不属于同一个集合则合并他们,并把他们算作最终结果
- 重复
2直到该图成为生成树(边的数量达到 $V-1$
//邻接矩阵的结构体
struct node{
int u,v,w;
bool operator<(const node &a)const{
return w<a.w;
}
} ph[inf];
int kruskal(){
//枚举边
for(int i=0;i<m;i++){
node p=ph[i];
if(find(p.u)!=find(p.v)){
f[find(p.u)]=find(p.v); //合并
ans+=p.w; //计算价值
c++;
if(c==n-1)
return ans; //返回结果
}
}
return ans;
}注意:调用之前需要先排序(sort(ph, ph + m) 在 <algorithm> 库中)。