当你碰到一个题,希望你找到一条从 $A$ 到 $B$ 的路径,且它总里程最短。
然而你暴力枚举一定是超时的。
所以现在我们就需要一个新的方法来计算。
Dijkstra
Dijkstra算法能够非常好的解决 $G=(V,E)$ 上带权的单源最短路径问题。
我们从源点 $s$ 到集合里面的顶点最终最短路径的权值都已经确定了,它反复将选择能成为最短路径上的出边 $u$ 放入集合 $S$ ,对于所有的出边 $u$ 进行松弛操作。
松弛
松弛就是能更新最短路径上面路径的最小值的方法。
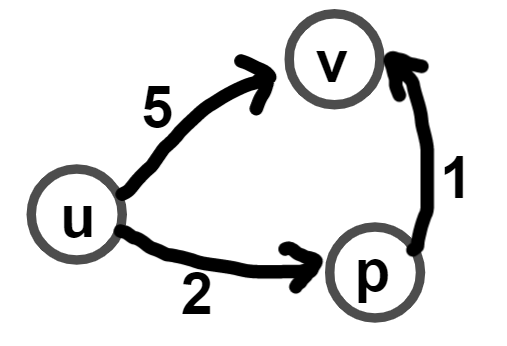
比如上图,我希望从 $u$ 直接前往 $v$ 即 $u \rightarrow v$ 的路程是 $5$ ,然后我们找到一个点 $p$ ,希望从 $u$ 通过点 $p$ 再到 $v$ 即 $u \rightarrow p \rightarrow v$ 的路程是 $3$ 。我们会选用第二种方法。
如果第二个方法比第一个路程更短,则将第一个的路程更新为第二个,否则跳过。
Dijkstra 的实现
每次在集合中选择一个(在集合内的)最小的边并将它移除集合,对他循环搜索所有可能进行松弛的方案进行松弛。
如果能进行松弛,就将新的边插入集合中,以此类推。
让我们来试试。从图中0号节点开始。
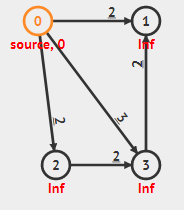
$0\rightarrow 1$ 更新1号,将1号的最小路径改为2。
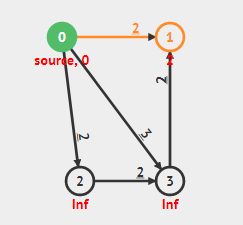
$0 \rightarrow 2$ 更新2号,将2的最小路径改为2。
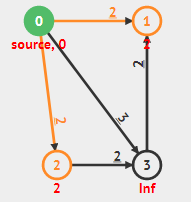
0号执行完成,去1号继续,1号无出边。
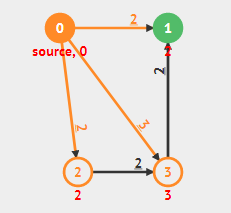
$1\rightarrow 3$ 去3号,更新3为3。
去2号继续。$2 \rightarrow 3$ 未能跟新3(原来是3,新值是2+2=4)。
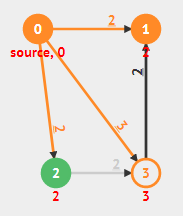
去3号继续,$3 \rightarrow 1$ 未能更新1(1原来就是2,新的值是3+2=5)。

到此为止,下图就是运行结束的最终结果。(0:0, 1:2, 2:2, 3:3)。

程序实现:
void dijstl()
{
//初始化
for (int i = 0; i <= n; i ++)
{
dis[i] = INF;
}
//插入开始节点 start
Node node = toNode(start, 0);
dis[start] = 0;
q.push(node);
//Dijkstra
while (!q.empty())
{
node = q.top(); //取出节点并删除
q.pop();
if (vis[node.pos]) //判断是否访问过
{
continue;
}
vis[node.pos] = true; //标记为访问过
for (int i = 0; i < adj[node.pos].size(); i ++)
{
//循环松弛
int v = adj[node.pos][i].v;
int w = adj[node.pos][i].w;
if (dis[node.pos] + w < dis[v])
{
dis[v] = dis[node.pos] + w;
Node tmp = toNode(v, dis[v]);
q.push(tmp);
}
}
}
}在上面代码中,用q即优先队列(priority_queue<int> q)来表示集合,他能自动给出一个最小的边;用adj存储原图(vector<int> adj[100]);d(int d[100])是用来统计从start开始的到所有点的最小值。
看一道题,洛谷 P4479
与上面思路完全一样,添加主函数即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <vector>
using namespace std;
const int inf = 2 * 1e5 + 5;
const int INF = 2147483647;
struct Edge //原始数据的数据结构
{
int v, w;
};
struct Node //优先队列的数据结构
{
int pos, w;
bool operator<(const Node &x)const //重载函数,用于优先队列比大小
{
return w > x.w;
}
};
inline Edge toEdge (int v, int w)
{
Edge tmp;
tmp.v = v, tmp.w = w;
return tmp;
}
inline Node toNode (int v, int w)
{
Node tmp;
tmp.pos = v, tmp.w = w;
return tmp;
}
vector <Edge> adj[inf];
priority_queue <Node> q;
int n, m, start, dis[inf], vis[inf];
void dijstl()
{
for (int i = 0; i <= n; i ++)
{
dis[i] = INF;
}
Node node = toNode(start, 0);
dis[start] = 0;
q.push(node);
while (!q.empty())
{
node = q.top();
q.pop();
if (vis[node.pos])
{
continue;
}
vis[node.pos] = true;
for (int i = 0; i < adj[node.pos].size(); i ++)
{
int v = adj[node.pos][i].v;
int w = adj[node.pos][i].w;
if (dis[node.pos] + w < dis[v])
{
dis[v] = dis[node.pos] + w;
Node tmp = toNode(v, dis[v]);
q.push(tmp);
}
}
}
}
int main ()
{
cin >> n >> m >> start; //输入
int u, v, w;
for (int i = 0; i < m; i ++)
{
cin >> u >> v >> w;
Edge tmp = toEdge(v, w); //创建原始数据
adj[u].push_back(tmp);
}
dijstl();
for (int i = 1; i <= n; i ++)
{
cout << dis[i] << " "; //输出所有的答案
}
return 0;
}